Here I assume a basic understanding of regular expressions with capturing groups (as supported in many programming languages), and the relevant basics about finite automatons: DFAs and NFAs. It also doesn't hurt looking at Russ Cox' excellent series on implementing regular expressions.
A few thoughts how to restrict regular expressions such that they are "composable" in the presence of capturing groups, in the following sense: Given a list R of length n of regular expressions (which may contain capturing groups), and given a list A of the same length such that A[i] ~ R[i] for i = 0 ... n-1 (i.e., each input matches its corresponding regular expression). Let A = A[0] ... A[n-1] and R = R[0] ... R[n-1] (i.e., textual concatentation of inputs and regular expressions). We demand that A ~ R (ok, that's always true) and the captured strings should be the same.
One popular application of regular expressions is splitting text records into their individual fields with capturing groups. For example to parse the file /etc/passwd on a UNIX system one can use a regex like
^([^:]*):([^:]*):([^:]*):([^:]*):([^:]*):([^:]*):([^:]*)$
Compiling and matching this expression against a line from /etc/passwd like
root:x:0:0:root:/root:/bin/bash
creates an array of the colon-separated fields which can then be further processed.
Now, there are many data types that are suitable for representation as text, and not all of them fit well in the pattern [^:]* (which matches any sequence of non-colon characters). It would be nice if we could allow general regular expressions as field parsers. But the problem with that is ambiguity: For example, let's suppose we have a string datatype which matches any sequence of characters (.*), and we want to parse lines that contain two such string values, separated by a space. The pattern to match lines against is
^(.*) (.*)$
What should be the two parsed fields after matching against the following line?
a b c
It could be either (a) (b c) or (a b) (c). Clearly that's a problem as soon as we care not only whether the line matched, but also what's in the capturing groups.
Typically regular expression implementations work around this ambiguity by making the repetition modifier (*) greedy, which means to consume as much text as possible while still allowing the rest of the regular expression to match. Some implementations also offer a non-greedy variant.
But that's still not a very usable approach from the standpoint of composition: It means that whether a given prefix of a line of text is matched as contents of the first field (capturing group) depends on the rest of the line, and whether that rest can be matched by the remainder of the regular expression.
Let's assume we have a regular expression R1 that matches input I1 and returns a list of captures L1, and similarly we have R2, I2, L2. While R1 + R2 is guaranteed to match I1 + I2, it is not guaranteed to return the capture list L1 + L2.
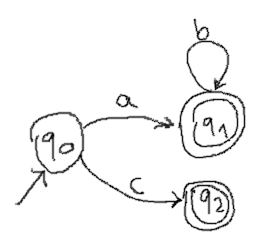
Some combinations of regular expressions are safe in that regard. For example, the /etc/passwd example above. To see what criterion must be met by a given pair of adjacent regular expressions to avoid ambiguity, let us now look at their NFA representations. Here is an NFA for the expression ab*|c.

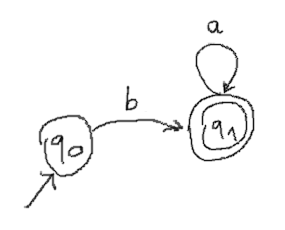
Here is another one for ba*:
Here is the automaton for their composition (ab*|c)(ba*). Composition works by connecting all accepting states from the first automaton to the initial state of the second automaton with an epsilon (= empty) transition. In the following image, transition labels are drawn in blue if they are part of the first automaton. They are drawn in red if they are part of the second automaton. Also the accept-markers are drawn in the respective colors. The "red-accepting" states (in this case only q4) are at the same time the accepting states for the composed automaton. The two captured values after an accepting match are the concatenations of all the traversed characters of the respective colors.
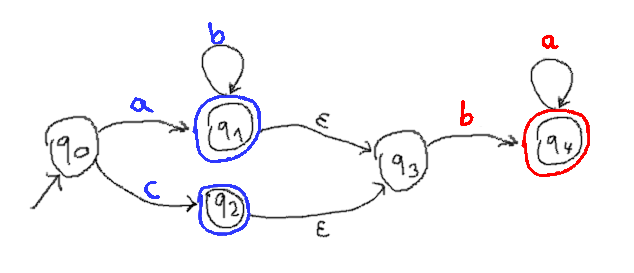
We can eliminate the epsilon transitions in the following way:
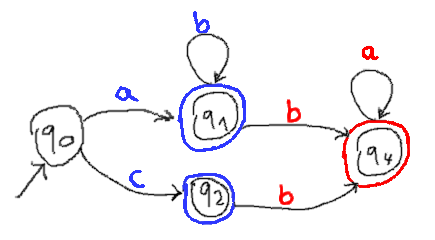
And the problem becomes obvious: If there are "blue-accepting" states with outgoing transitions for the same character in different colors, there is ambiguity.
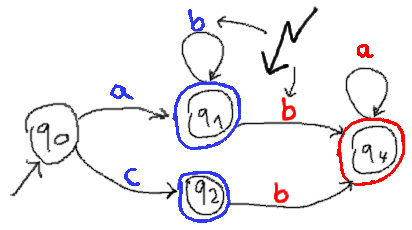
In fact, there is even ambiguity if any two blue accepting states have outgoing transitions for the same character in different colors, given that they can be reached through a common input. In the given example there is no input that leads to both q1 and q2, so the blue b-transition from q1 does not conflict with the red b-transition from q2.
To remove ambiguity we can add separators in between (which need not be in a capturing group). The following example matches (ab*|c)x(ba*):
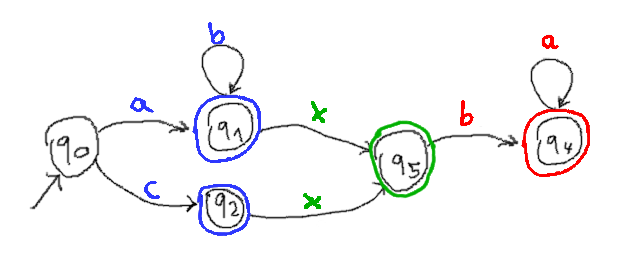
With this approach the second (red) automaton can be anything, without ambiguity. That does of course only work because the separator character is on no blue transition outgoing from a blue accepting state.
Created 2017-04-14Updated 2018-07-10