Working on my own Red-black tree implementation, I found that starting with a blank slate, there are a few tricks that lead to simplified code vs what reference material I found elsewhere on the internet. On this page I'm writing down some of these improvements. In particular there is a nice drawing at the end which helps keeping the program logic clean, and "Array of child pointers" is a really important technique not employed in many implementations.
As of 2019, a complete implementation of a 3-pointer Red-Black tree lives lives here: http://jstimpfle.de/projects/rb3ptr/rb3ptr.html.
Generally you want an intrusively linked data structure. Intrusive linking means that the user of the tree is required to embed a link-head structure, which contains child and parent pointers, in each node that should be linked in a tree. Most tree functionality (excluding node comparison, of course) can then be implemented in ignorance of the actual payload.
The advantages of intrusive linking include generic (machine) code, not having to care about memory allocation in the implementation, and the client code being able to link data in multiple structures at once in a cache friendly way. I won't go more into this; if you are interested look into my implementation or the linux doubly linked list (list.h) or Red-black tree (rbtree.c). Recently there was also a thread on Hacker News with many good arguments for intrusive linking.
Broadly speaking there are 2-pointer and 3-pointer red-black trees. The 2-pointer versions have only left- and right-child pointers in each tree node, while the 3-pointer versions have an additional parent pointer. The parent pointer enables following the path to the root, which is needed to rebalance the tree after insertions and deletions. The 2-pointer version has no parent-pointers, so when inserting or deleting a node one first needs to search the relevant place in the tree, starting from the root of the tree, and recording the path in a stack of node pointers. This probably means that 2-pointer approaches are less suited for concurrent accesses because the recorded path must not be invalidated during the rebalancing. Furthermore having to search the node first can be an annoying inefficiency, however the saved memory seems to bring a net win in time for trees containing up to a few hundred thousand elements on modern machines.
A really useful technique that I found on the internet is storing the left- and right-child pointers in an array of length two instead of having members named "left" and "right". That array is of course subscripted with the integers 0 and 1, which is useful because these are C's (and, in a sense, CPUs') true and false.
struct rb2_head {
struct rb2_head *ptr[2];
};
This simplifies the code a little: Code like this
if (parent->left == head)
dir == RB_LEFT;
else
dir == RB_RIGHT;
/* or this */
if (dir == RB_LEFT)
head = head->left;
else
head = head->right;
becomes this
dir = parent->right == head;
/* or this */
head = head->ptr[dir];
The biggest benefit is the following, though: The symmetric variants need not be implemented. In the rebalancing code we just make two variables left and right. These can be 0/1 or 1/0 when the rebalancing happens, and the code for each case works for both symmetric variants.
I learned this trick from Julienne Walker (eternallyconfuzzled.com). Thank you Julienne for posting your articles, especially the top-down Red-black tree.
The conventional approach to space-efficient implementation is to store the node color (red or black, which is 1 bit) in an unused bit of the node pointers (left/right/parent). I've taken this a step further: instead of storing each node's own color we can store the childs' colors using one bit of each pointer. This should in theory save a few cache misses during rebalancings (since some childs don't have to be accessed), but I don't know yet if the effects can be seen in benchmarks.
Put differently, we store the colors on the edges, not in the nodes. A nice side effect of this is that leaves (which are always black) can be represented by NULL pointers without requiring a special case for color testing.
Another idea I had which brought a slight simplification to the implementation is storing the direction from the parent to the current node (left or right) in an unused bit of the parent pointer (in the 3-pointer version). This renders the first part of the above code example unnecessary. I don't expect a difference in performance, though I don't have a conventional implementation for comparison.
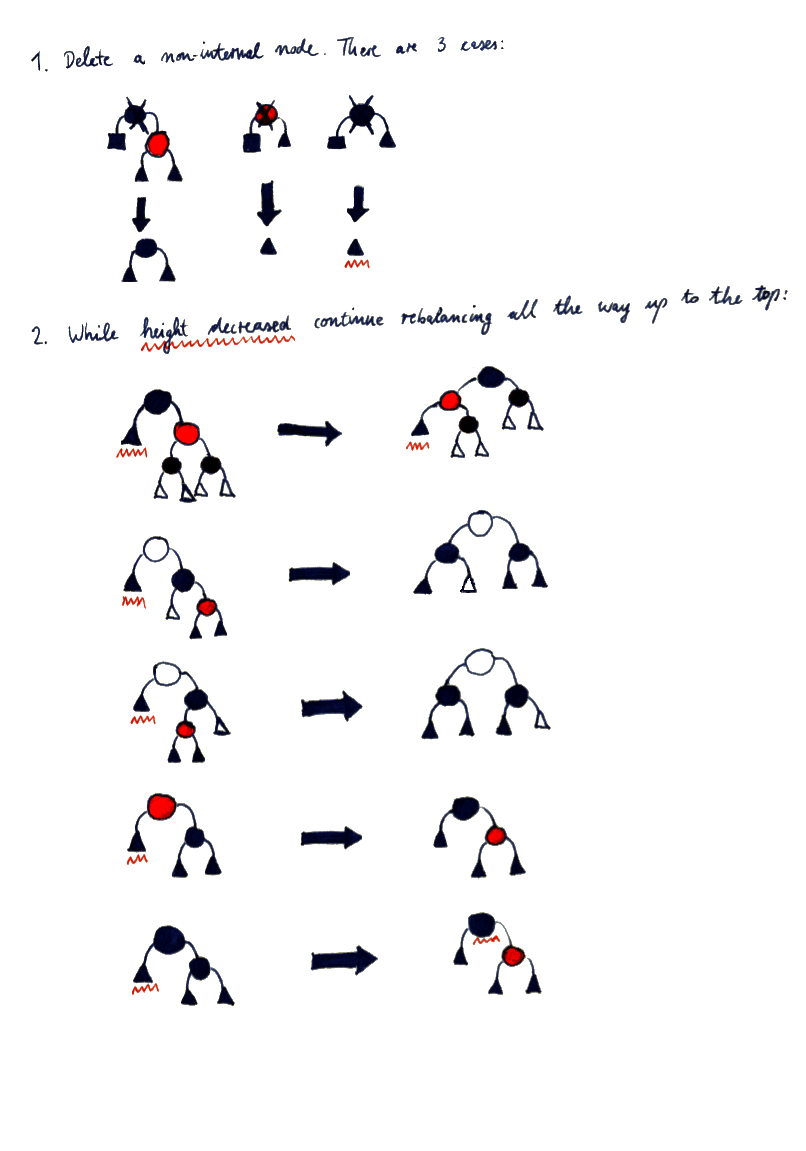
Deletion from Red-black trees is quite complicated. I looked at the German and English Wikipedia articles and decided to make a condensed variant, i.e. a cheat sheet. Illustrating the transformations without the exhausting detail and formal reasoning found in most places goes a long way for ease of implementation.
I noticed that it's much easier *not* to think in rotations, and to avoid multi-step transformations where possible. Having only a view of the relevant section of an imbalanced tree, and how it should look after transformation, brings a decrease in the "implementation distance" that has to be bridged. And it shows: many other implementations you can find on the internet clearly used Wikipedia as a basis — they have more complex control flow and redundant assignments.
For an implementation based on the drawing below, you need to understand at least the Red-black tree height invariant, and how to remove internal nodes from general binary search trees by replacing them with their in-order predecessor/successor. You probably should also try and understand why each case is balanced after transformation (unless zig-zagged in red). If that's not clear, refer to Wikipedia.
Instructions: Circles are non-leaf nodes, squares are leaves (which are always black), and triangles are subtrees (which could be leaves). The nodes don't have names. Names are not necessary because the transformations must preserve the horizontal ordering. Only the vertical ordering and the colors change. A white node or subtree means "unknown color". A white node after transformation means "same color as before" (although that color could be applied to a different node).
This sheet contains all cases except for the symmetric variants. Check all cases in the order of presentation, by only checking for red nodes. Each case except for the last is one color test.
For reference, here is my 3-pointer delete-rebalance procedure compared to the linux implementation. Note that the linux version (which is far from the worst I could find) makes heavy use of the WRITE_ONCE macro due to the complex memory model in the kernel — but I don't believe that it adds to the number of lines.
static void rb3_delete_rebalance(struct rb3_head *head)
{
struct rb3_head *pnt;
struct rb3_head *gpnt;
struct rb3_head *sibling;
struct rb3_head *sleft;
struct rb3_head *sleftleft;
struct rb3_head *sleftright;
int left;
int right;
int gdir;
if (!rb3_get_parent(head))
return;
if (!rb3_get_parent(rb3_get_parent(head)))
return;
pnt = rb3_get_parent(head);
left = rb3_get_parent_dir(head);
right = !rb3_get_parent_dir(head);
gpnt = rb3_get_parent(pnt);
gdir = rb3_get_parent_dir(pnt);
sibling = rb3_get_child(pnt, right);
sleft = rb3_get_child(sibling, left);
if (rb3_is_red(pnt, right)) {
rb3_connect(pnt, right, sleft, RB3_BLACK);
rb3_connect(sibling, left, pnt, RB3_RED);
rb3_connect(gpnt, gdir, sibling, RB3_BLACK);
rb3_delete_rebalance(head);
} else if (rb3_is_red(sibling, right)) {
rb3_connect_null(pnt, right, sleft, rb3_get_color_bit(sibling, left));
rb3_connect(sibling, left, pnt, RB3_BLACK);
rb3_connect(gpnt, gdir, sibling, rb3_get_color_bit(gpnt, gdir));
rb3_set_black(sibling, right);
} else if (rb3_is_red(sibling, left)) {
sleftleft = rb3_get_child(sleft, left);
sleftright = rb3_get_child(sleft, right);
rb3_connect_null(pnt, right, sleftleft, RB3_BLACK);
rb3_connect_null(sibling, left, sleftright, RB3_BLACK);
rb3_connect(sleft, left, pnt, RB3_BLACK);
rb3_connect(sleft, right, sibling, RB3_BLACK);
rb3_connect(gpnt, gdir, sleft, rb3_get_color_bit(gpnt, gdir));
} else if (rb3_is_red(gpnt, gdir)) {
rb3_set_red(pnt, right);
rb3_set_black(gpnt, gdir);
} else {
rb3_set_red(pnt, right);
rb3_delete_rebalance(pnt);
}
}
|
static void rb_erase_color(struct rb_node *parent, struct rb_root *root)
{
struct rb_node *node = NULL;
struct rb_node *sibling;
struct rb_node *tmp1;
struct rb_node *tmp2;
while (true) {
sibling = parent->rb_right;
if (node != sibling) {
if (rb_is_red(sibling)) {
tmp1 = sibling->rb_left;
WRITE_ONCE(parent->rb_right, tmp1);
WRITE_ONCE(sibling->rb_left, parent);
rb_set_parent_color(tmp1, parent, RB_BLACK);
__rb_rotate_set_parents(parent, sibling, root, RB_RED);
sibling = tmp1;
}
tmp1 = sibling->rb_right;
if (!tmp1 || rb_is_black(tmp1)) {
tmp2 = sibling->rb_left;
if (!tmp2 || rb_is_black(tmp2)) {
rb_set_parent_color(sibling, parent, RB_RED);
if (rb_is_red(parent))
rb_set_black(parent);
else {
node = parent;
parent = rb_parent(node);
if (parent)
continue;
}
break;
}
tmp1 = tmp2->rb_right;
WRITE_ONCE(sibling->rb_left, tmp1);
WRITE_ONCE(tmp2->rb_right, sibling);
WRITE_ONCE(parent->rb_right, tmp2);
if (tmp1)
rb_set_parent_color(tmp1, sibling, RB_BLACK);
tmp1 = sibling;
sibling = tmp2;
}
tmp2 = sibling->rb_left;
WRITE_ONCE(parent->rb_right, tmp2);
WRITE_ONCE(sibling->rb_left, parent);
rb_set_parent_color(tmp1, sibling, RB_BLACK);
if (tmp2)
rb_set_parent(tmp2, parent);
__rb_rotate_set_parents(parent, sibling, root, RB_BLACK);
break;
} else {
sibling = parent->rb_left;
if (rb_is_red(sibling)) {
tmp1 = sibling->rb_right;
WRITE_ONCE(parent->rb_left, tmp1);
WRITE_ONCE(sibling->rb_right, parent);
rb_set_parent_color(tmp1, parent, RB_BLACK);
__rb_rotate_set_parents(parent, sibling, root, RB_RED);
sibling = tmp1;
}
tmp1 = sibling->rb_left;
if (!tmp1 || rb_is_black(tmp1)) {
tmp2 = sibling->rb_right;
if (!tmp2 || rb_is_black(tmp2)) {
rb_set_parent_color(sibling, parent, RB_RED);
if (rb_is_red(parent))
rb_set_black(parent);
else {
node = parent;
parent = rb_parent(node);
if (parent)
continue;
}
break;
}
tmp1 = tmp2->rb_left;
WRITE_ONCE(sibling->rb_right, tmp1);
WRITE_ONCE(tmp2->rb_left, sibling);
WRITE_ONCE(parent->rb_left, tmp2);
if (tmp1)
rb_set_parent_color(tmp1, sibling, RB_BLACK);
tmp1 = sibling;
sibling = tmp2;
}
tmp2 = sibling->rb_right;
WRITE_ONCE(parent->rb_left, tmp2);
WRITE_ONCE(sibling->rb_right, parent);
rb_set_parent_color(tmp1, sibling, RB_BLACK);
if (tmp2)
rb_set_parent(tmp2, parent);
__rb_rotate_set_parents(parent, sibling, root, RB_BLACK);
break;
}
}
}
|
Since this worked out so nicely, another cheat sheet for insertion would be nice (TODO!). Insertion is a little simpler, though, and my implementations were done straight from Wikipedia without much trouble, but in the spirit of the deletion implementation.
To come for completeness.
Created: 2017-04-17
Updated: 2021-02-28